Climbing Ranked Mode in Pokémon TCG Pocket

Last month, Pokémon TCG Pocket introduced a new ranked mode, and like many, I dove headfirst into it. But also like many, I hit a wall when I reached Ultra Ball. The grind to Master Ball just felt impossible, even going in with a 70% win-rate deck. Against other meta decks, matches felt more like coin-flips than actual strategy. I was left wondering: how long would it take to reach Master Ball if I had a deck that was literally a coin-flip? What about a weighted coin-flip?

Let’s do some back-of-the-napkin math.

Ranked Mode Basics

First, let’s cover the basics of ranked mode. Players start at Beginner Rank 1 and can progress to Master Ball Rank. Each rank has four tiers, except for Master Ball, which is the final rank.

Players progress through ranks by earning points from matches:

Rank

Points

Beginner Rank 1

0

Beginner Rank 2

20

Beginner Rank 3

50

Beginner Rank 4

95

Poke Ball Rank 1

145

Poke Ball Rank 2

195

Poke Ball Rank 3

245

Poke Ball Rank 4

300

Great Ball Rank 1

355

Great Ball Rank 2

420

Great Ball Rank 3

490

Great Ball Rank 4

600

Ultra Ball Rank 1

710

Ultra Ball Rank 2

860

Ultra Ball Rank 3

1010

Ultra Ball Rank 4

1225

Master Ball Rank

1450

Points per Match

  • Win: 10 points

  • Loss:

    • Beginner: no penalty

    • Poke Ball & Great Ball: -5 points

    • Ultra Ball & Master Ball: -7 points

Win-Streak Bonuses

Consecutive wins grant extra points (up to Great Ball Rank 4):

Consecutive Wins

Bonus

2

+3

3

+6

4

+9

5 or more

+12

Expected Points per Match

Think of each match as a weighted coin flip with probability \(p\) of winning. The expected points per match are:

\[ \mathbb{E}[\text{PointsPerMatch}(r, p)] = p \times \text{reward} - (1 - p) \times \text{penalty}_r \]

For example, at Poke Ball rank with a 60% win rate:

\[ \mathbb{E}[\text{PointsPerMatch}(\text{Poke Ball}, 0.6)] = 0.6 \times 10 - 0.4 \times 5 = 4 \]

At 60% win-rate, you’d average 4 points per match.

Adding Win-Streak Bonuses

To calculate streak bonuses, consider the probability of having exactly an \(n\)-win streak at any time. Each streak scenario (exactly \(n\) wins after a loss) has probability:

For example, a loss followed by 2 wins would be:

\[\begin{split} \begin{aligned} P(LW^2) &= P(L) \times P(W) \times P(W) \\ &= (1 - p) \times p \times p \\ &= (1 - p)p^2 \end{aligned} \end{split}\]

Or, more generally, for exactly \(n\) wins after a loss:

\[ P(LW^n) = (1 - p)p^n \]

For Streaks greater than 5

The caveat is that we need to consider the probability of being on a streak of 5 or more wins. This is a little different because it includes all the probabilities of being on a 5-win streak, a 6-win streak, and so on. But we can simplify it using the formula for the sum of a geometric series.

\[\begin{split} \begin{aligned} P(LW^{\geq 5}) &= (1 - p)p^5 + (1 - p)p^6 + (1 - p)p^7 + \dots \\ &= (1 - p)p^5 \times \left(1 + p + p^2 + \dots\right) \\ &= (1 - p)p^5 \times \frac{1}{1 - p} \\ &= p^5 \\[6pt] \end{aligned} \end{split}\]

Summing It Up

We can now easily compute the expected streak bonus at win probability \(p\):

Consecutive Wins

Bonus

Probability

2

+3

\((1 - p)p^2\)

3

+6

\((1 - p)p^3\)

4

+9

\((1 - p)p^4\)

5+

+12

\(p^5\)

Summing multiply the probabilities by their respective bonuses gives us the expected streak bonus:

\[ \mathbb{E}[\text{StreakBonus}(p)] = 3(1 - p)p^2 + 6(1 - p)p^3 + 9(1 - p)p^4 + 12p^5 \]

Simplified a bit more neatly:

\[ (1 - p)(3p^2 + 6p^3 + 9p^4) + 12p^5 \]

For a quick reference, here’s what that looks like at different win-rates \(p\):

Win Rate

Expected Streak Bonus

0.50

1.41

0.60

2.35

0.70

3.72

0.80

5.67

0.90

8.36

1.00

12.00

But now, we end up with a final formula for the expected points per match w/ win-streak bonuses by adding it to our win scenario:

\[ P(W) \times \text{reward} + \text{StreakBonus}(p) - P(L) \times \text{penalty}_r \]

Note that StreakBonus is separate from the win/loss probabilities because it already includes the probabilities of winning the given match.

And when filled in with our above work:

\[\begin{split} p \times \text{Reward}(r) + (1 - p)(3p^2 + 6p^3 + 9p^4) + 12p^5 - (1 - p) \times \text{Penalty}(r) \\[6pt] \\ \end{split}\]

Let’s Code It Up

import pandas as pd

WIN_RATES = [0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
"""Set a list of win rates to test."""

REWARD = 10
"""All ranks get 10 points for a win"""


def penalty_points(r):
    """Get the penalty points for a given rank."""
    if r.startswith("Beginner") or r.startswith("Poke"):
        return 0
    if r.startswith("Great"):
        return 5
    if r.startswith("Ultra") or r.startswith("Master"):
        return 7
    raise ValueError(f"Unknown rank: {r}")


def has_streak_bonus(r):
    """Check if a rank has a streak bonus."""
    return r.startswith("Beginner") or r.startswith("Poke") or r.startswith("Great")


def streak_bonus(p):
    """Calculate the streak bonus for a given win rate."""
    return (1 - p) * (3 * p**2 + 6 * p**3 + 9 * p**4) + 12 * p**5


def expected_points(r, p):
    """Calculate the expected points per match for a given rank and win rate."""
    penalty = penalty_points(r)
    if has_streak_bonus(r):
        return p * REWARD + streak_bonus(p) - (1 - p) * penalty
    else:
        return p * REWARD - (1 - p) * penalty

df = pd.DataFrame(
    {
        "Rank": ["Beginner", "Poke Ball", "Great Ball", "Ultra Ball", "Master Ball"],
    }
)

for p in WIN_RATES:
    df[f"Points per Match ({int(p*100)}%)"] = df.apply(
        lambda row: expected_points(row["Rank"], p), axis=1
    )

print(df.to_markdown(index=False, floatfmt=".2f"))

From this we can really see how the expected points drops off as we move up the ranks, especially when we lose the streak bonuses:

Rank

Points per Match (50%)

Points per Match (60%)

Points per Match (70%)

Points per Match (80%)

Points per Match (90%)

Points per Match (100%)

Beginner

6.41

8.35

10.72

13.67

17.36

22.00

Poke Ball

6.41

8.35

10.72

13.67

17.36

22.00

Great Ball

3.91

6.35

9.22

12.67

16.86

22.00

Ultra Ball

1.50

3.20

4.90

6.60

8.30

10.00

Master Ball

1.50

3.20

4.90

6.60

8.30

10.00

Interestingly, if Ultra Ball had a streak bonus, a deck with a 50% win-rate would almost double its expected points per match from \(1.5\) to \(2.91\)!

\[\begin{split} \begin{aligned} \mathbb{E}[\text{PointsPerMatch}(\text{Ultra Ball}, 0.5)] &= 0.5 \times 10 - 0.5 \times 7 \\ &= 1.5 \\ \mathbb{E}[\text{StreakBonus}(0.5)] &= (1 - 0.5)(3 \times 0.5^2 + 6 \times 0.5^3 + 9 \times 0.5^4) + 12 \times 0.5^5 \\ &= 1.41 \\[6pt] \end{aligned} \end{split}\]

How Many Matches to Rank Up?

Let’s say I’ve just hit Great Ball Rank 3 (490 points), and I have a solid 60% win-rate deck. How many matches will I need to reach Great Ball Rank 4 (600 points)?

Well, now that we have the expected points per match, we can calculate the number of matches needed to reach the next rank.

\[\begin{split} \begin{aligned} \text{PointsNeeded}(r) &= \text{Points}_{r_{curr}} - \text{Points}_{r_{next}} \\[6pt] \mathbb{E}[\text{Matches}(r, p)] &= \frac{\text{PointsNeeded}(r)}{\mathbb{E}[\text{PointsPerMatch}(r, p)]} \end{aligned} \end{split}\]

In the case of Great Ball Rank 3 to Great Ball Rank 4:

\[\begin{split} \begin{aligned} &= \frac{600 - 490}{\mathbb{E}[\text{PointsPerMatch}(\text{Great Ball Rank 3}, 0.6)]} \\[6pt] &= \frac{600 - 490}{6.35} \\[6pt] &\approx 17.32 \end{aligned} \end{split}\]

This means, on average, I need to play 17.32 matches to rank up from Great Ball Rank 3 to Great Ball Rank 4 with a 60% win-rate deck.

Coding It Up

Let’s now do this for every rank for both getting to the next rank and the total number of matches needed to reach that rank.

df = pd.DataFrame(
    data=[
        ("Beginner 1", 0),
        ("Beginner 1", 20),
        ("Beginner 1", 50),
        ("Beginner 1", 95),
        ("Poke Ball 1", 145),
        ("Poke Ball 2", 195),
        ("Poke Ball 3", 245),
        ("Poke Ball 4", 300),
        ("Great Ball 1", 355),
        ("Great Ball 2", 420),
        ("Great Ball 3", 490),
        ("Great Ball 4", 600),
        ("Ultra Ball 1", 710),
        ("Ultra Ball 2", 860),
        ("Ultra Ball 3", 1010),
        ("Ultra Ball 4", 1225),
        ("Master Ball", 1450),
    ],
    columns=["Rank", "Points"],
)

df["Points Diff."] = df["Points"].diff().fillna(0).astype(int)

for p in WIN_RATES:
    df[f"Matches ({int(p*100)}%)"] = df.apply(
        lambda row: row["Points Diff."] / expected_points(row["Rank"], p), axis=1
    )

Rank

Matches (50%)

Matches (60%)

Matches (70%)

Matches (80%)

Matches (90%)

Matches (100%)

Beginner 1

0.00

0.00

0.00

0.00

0.00

0.00

Beginner 1

3.12

2.40

1.87

1.46

1.15

0.91

Beginner 1

4.68

3.59

2.80

2.19

1.73

1.36

Beginner 1

7.02

5.39

4.20

3.29

2.59

2.05

Poke Ball 1

7.80

5.99

4.66

3.66

2.88

2.27

Poke Ball 2

7.80

5.99

4.66

3.66

2.88

2.27

Poke Ball 3

7.80

5.99

4.66

3.66

2.88

2.27

Poke Ball 4

8.59

6.59

5.13

4.02

3.17

2.50

Great Ball 1

14.08

8.66

5.96

4.34

3.26

2.50

Great Ball 2

16.64

10.24

7.05

5.13

3.86

2.95

Great Ball 3

17.92

11.02

7.59

5.53

4.15

3.18

Great Ball 4

28.16

17.32

11.93

8.68

6.53

5.00

Ultra Ball 1

73.33

34.38

22.45

16.67

13.25

11.00

Ultra Ball 2

100.00

46.88

30.61

22.73

18.07

15.00

Ultra Ball 3

100.00

46.88

30.61

22.73

18.07

15.00

Ultra Ball 4

143.33

67.19

43.88

32.58

25.90

21.50

Master Ball

150.00

70.31

45.92

34.09

27.11

22.50

And cummulatively…

for p in WIN_RATES:
    df[f"Matches ({int(p*100)}%)"] = df[f"Matches ({int(p*100)}%)"].cumsum()

Rank

Matches (50%)

Matches (60%)

Matches (70%)

Matches (80%)

Matches (90%)

Matches (100%)

Beginner 1

0.00

0.00

0.00

0.00

0.00

0.00

Beginner 1

3.12

2.40

1.87

1.46

1.15

0.91

Beginner 1

7.80

5.99

4.66

3.66

2.88

2.27

Beginner 1

14.83

11.38

8.86

6.95

5.47

4.32

Poke Ball 1

22.63

17.37

13.52

10.61

8.35

6.59

Poke Ball 2

30.44

23.35

18.18

14.27

11.23

8.86

Poke Ball 3

38.24

29.34

22.85

17.93

14.12

11.14

Poke Ball 4

46.83

35.93

27.98

21.95

17.28

13.64

Great Ball 1

60.91

44.59

33.94

26.29

20.55

16.14

Great Ball 2

77.55

54.83

40.99

31.42

24.40

19.09

Great Ball 3

95.47

65.85

48.58

36.95

28.56

22.27

Great Ball 4

123.63

83.17

60.50

45.63

35.08

27.27

Ultra Ball 1

196.96

117.55

82.95

62.30

48.33

38.27

Ultra Ball 2

296.96

164.42

113.56

85.03

66.41

53.27

Ultra Ball 3

396.96

211.30

144.17

107.75

84.48

68.27

Ultra Ball 4

540.30

278.48

188.05

140.33

110.38

89.77

Master Ball

690.30

348.80

233.97

174.42

137.49

112.27

This starts to highlight just why Ranked is so brutal. Even a very good deck with an 70% win-rate is going to take 233 matches to reach Master Ball!

If we visualize the cumulative matches needed to reach each rank, we can see how the difficulty ramps up at the Ultra Ball ranks when we lose the streak bonuses and the penalties increase.

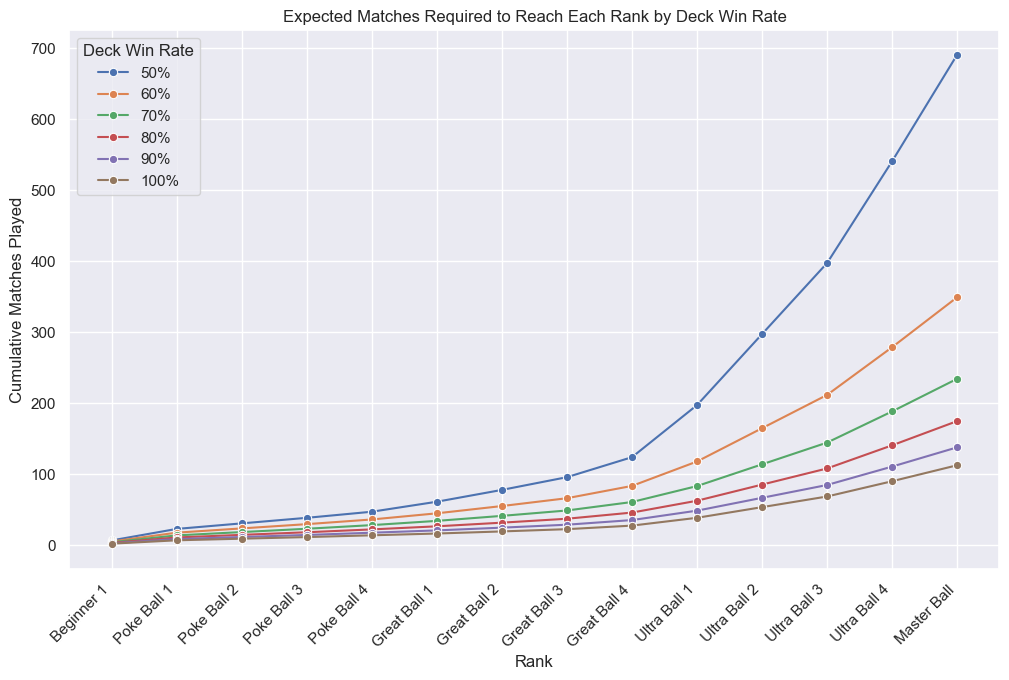
alt text

Time Spent

As someone with a day job, the thought has crossed my mind: “How many hours am I investing here?” Let’s break it down assuming that a match is an average of 5 minutes including matching time and setup and just focusing on how long it takes to get to the first tier of each ball.

TIME_PER_MATCH_S = 5 * 60  # 5 minutes per match

for p in WIN_RATES:
    df[f"Hours ({int(p*100)}%)"] = df[f"Matches ({int(p*100)}%)"] * TIME_PER_MATCH_S / 3600

Rank

Hours (50%)

Hours (60%)

Hours (70%)

Hours (80%)

Hours (90%)

Hours (100%)

Beginner 1

0.00

0.00

0.00

0.00

0.00

0.00

Beginner 1

0.26

0.20

0.16

0.12

0.10

0.08

Beginner 1

0.65

0.50

0.39

0.30

0.24

0.19

Beginner 1

1.24

0.95

0.74

0.58

0.46

0.36

Poke Ball 1

1.89

1.45

1.13

0.88

0.70

0.55

Poke Ball 2

2.54

1.95

1.52

1.19

0.94

0.74

Poke Ball 3

3.19

2.45

1.90

1.49

1.18

0.93

Poke Ball 4

3.90

2.99

2.33

1.83

1.44

1.14

Great Ball 1

5.08

3.72

2.83

2.19

1.71

1.34

Great Ball 2

6.46

4.57

3.42

2.62

2.03

1.59

Great Ball 3

7.96

5.49

4.05

3.08

2.38

1.86

Great Ball 4

10.30

6.93

5.04

3.80

2.92

2.27

Ultra Ball 1

16.41

9.80

6.91

5.19

4.03

3.19

Ultra Ball 2

24.75

13.70

9.46

7.09

5.53

4.44

Ultra Ball 3

33.08

17.61

12.01

8.98

7.04

5.69

Ultra Ball 4

45.02

23.21

15.67

11.69

9.20

7.48

Master Ball

57.52

29.07

19.50

14.53

11.46

9.36

alt text

And there’s our answer, with even a healthy 60% win-rate deck, expect to spend 29 hours to reach Master Ball vs a mear 10 hours for Ultra Ball. And chances are, your deck will manage a higher win-rate in the lower ranks.

This has confirmed my deep down suspicion that Master Ball just is not worth it. The grind is real and the rewards are not. At the end of this season, I will wear my Ultra Ball badge with pride.

Previous: Which Eevee is Actually Worth Playing?